3.3 线性回归简洁实现

flowchart LR
    A("开始") --> B["随机yield一批样本"]
   B --> C("计算该批下的平均损失（向前传播）")
     C --> D("计算参数梯度（向后传播）")
     D --> E("更新参数")
     E --> |"把整个样本都遍历一遍为止"|B

1. 生成数据集

和 3.2 线性回归从零开始实现#^6ae8e0 一样，根据预设定的数据增加噪声生成训练数据

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

2. 读取数据集

利用 Pytorch 的 data 模块（Pytorch 用法#^4a13ad）读取，并创造一个可以按 batch_size yield 出样本的迭代器：

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

3. 定义模型

我们首先定义一个模型变量 net，它是一个 Sequential 类的实例。 Sequential 类将多个层串联在一起。这里只要一层：

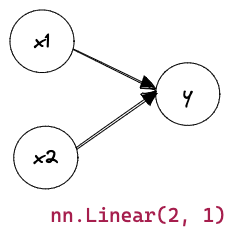
 # nn是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))
print(net) 
# 输出：
# Sequential(
#  (0): Linear(in_features=2, out_features=1, bias=True)
#) 

4. 初始化参数

通过net[0]选择网络中的第一个图层， 然后使用weight.data和bias.data方法访问参数

net[0].weight.data.normal_(0, 0.01) #从正态分布中选参数
net[0].bias.data.fill_(0)

以下划线结尾的方法修改参数 (2.1 数据操作#^cfee62)

5. 定义损失函数

loss = nn.MSELoss()

均方误差（Pytorch 中的损失函数#^b31bac）默认情况下，它返回所有样本损失的平均值（平均的目的是保持一致的学习率），是一个标量

6. 定义优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

• 优化器：随机梯度下降，注意其实是批量梯度下降算法，随机在DataLoader 3.3 线性回归简洁实现#^31289d 决定，详见 Pytorch 用法#^c3b356
• 输入参数：网络中的参数（这里的 net.parameters() 是个可迭代对象）、学习率
• 由 trainer 统一负责网络中参数管理

7. 训练

在每个迭代周期里，我们将完整遍历一次数据集（train_data），不停地从中获取一个小批量的输入和相应的标签。对于每一个小批量，我们会进行以下步骤:

• 通过调用net(X)生成预测并计算损失l（前向传播）。
• 通过进行反向传播来计算梯度。
• 通过调用优化器来更新模型参数。

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad() 
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

参考文献