3.4 softmax 回归

1. 分类问题的独热编码

分类问题本身就是不连续的，直接用离散变量会导致损失函数不可导。统计学家很早以前就发明了一种表示分类数据的简单方法：独热编码（one-hot encoding）。独热编码是一个向量，它的分量和类别一样多。类别对应的分量设置为1，其他所有分量设置为0。在我们的例子中，标签 $y$ 将是一个三维向量，其中 $(1,0,0)$ 对应于“猫”、$(0,1,0)$ 对应于“鸡”、$(0,0,1)$ 对应于“狗”：

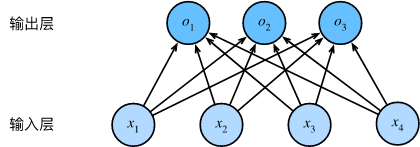
2. 网络架构

我们可以用神经网络图来描述这个计算过程。与线性回归一样，softmax 回归也是一个单层神经网络。由于计算每个输出 $o_1$、$o_2$ 和 $o_3$ 取决于所有输入 $x_1$、$x_2$、$x_3$ 和 $x_4$，所以 softmax 回归的输出层也是全连接层。

3. softmax 运算

实际上全连接层依旧是个线性模型，为了和 $(1,0,0)$ 这种分布进行比较差异，需要人为的将全连接结果转化为概率，一种比较好的函数就是 softmax 函数：

4. 对于多样本的矢量化

为了提高计算效率并且充分利用GPU，我们通常会对小批量样本的数据执行矢量计算。softmax回归的矢量计算表达式为：

向量化示意图，3.2 线性回归从零开始实现就是 4*1 的矩阵

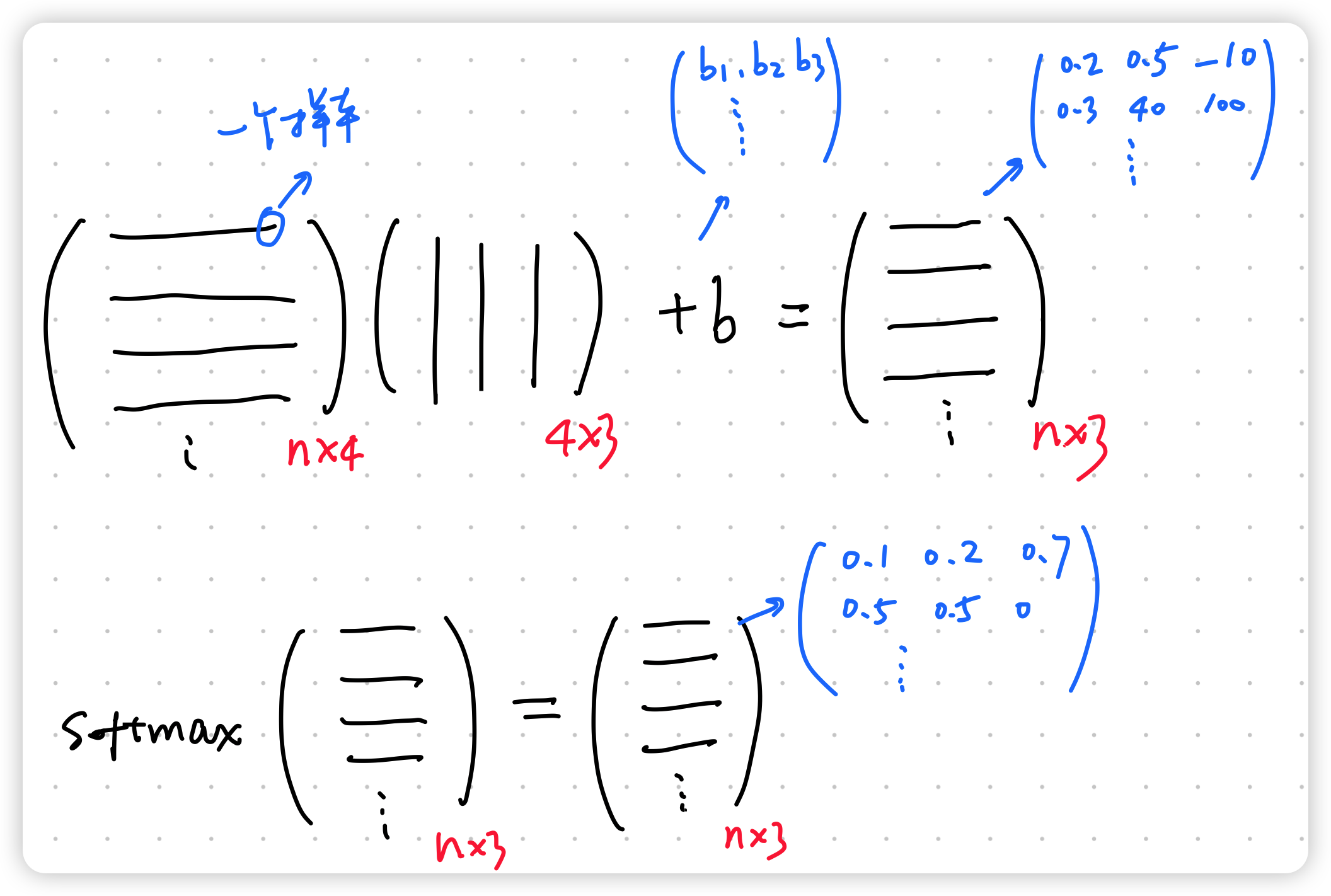
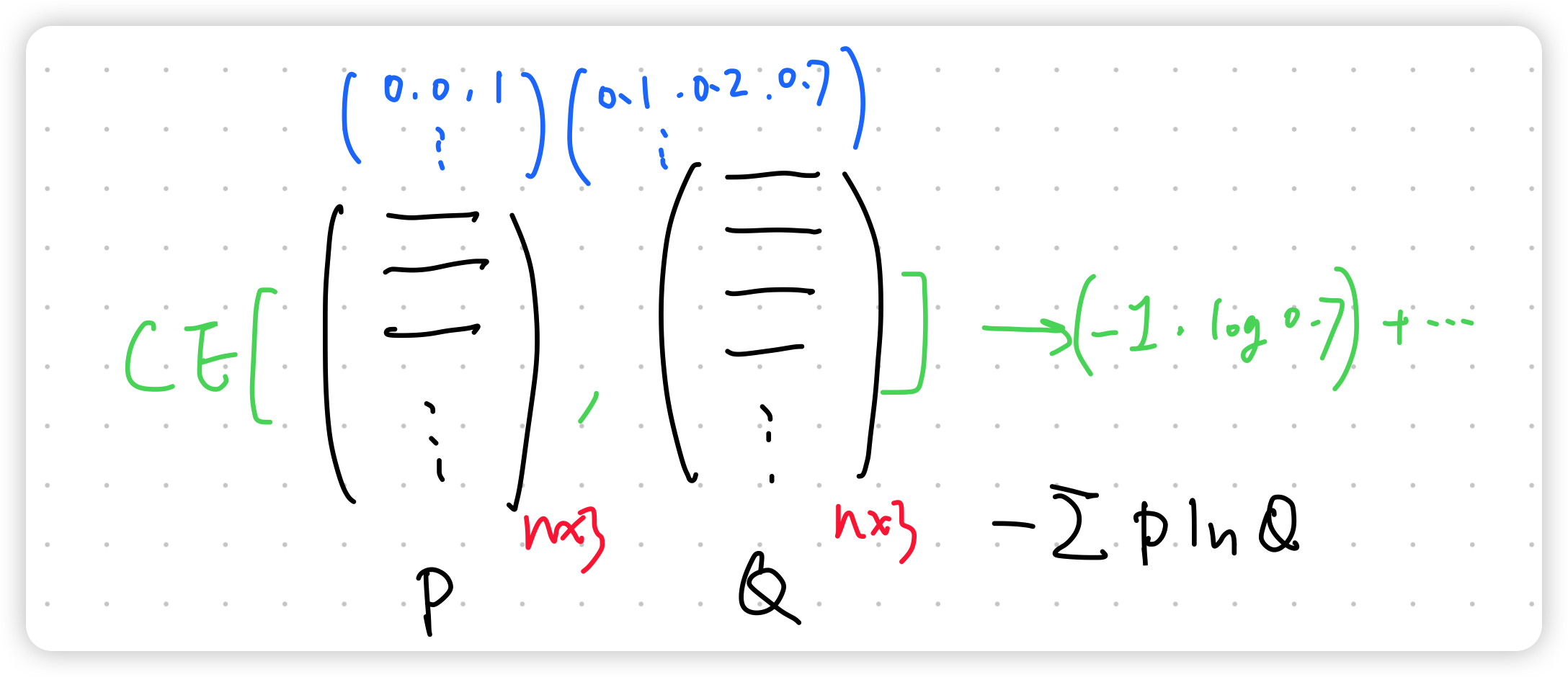
5. 损失函数：交叉熵

最后其实就是分布的差异，交叉熵等价于计算 KL 散度（信息熵（information entropy）#^17aaeb），示意图如下所示：
softmax 计算示意图

参考文献