4.1 多层感知机 MLP

要点

线性模型是个强假设，激活函数是非线性拟合的核心
通用近似原理：激活函数为单个隐藏层的 sigmoid 函数就已经能拟合任意函数了
沐神理解：MLP 是一个复杂度很强的模型，但很容易过拟合，造成不好调参，实际用得不多

1. 线性模型可能会出错

softmax 回归 3.4 softmax 回归的本质还是线性回归，softmax 函数只是为了转化为概率计算损失，和均方误差是类似的，线性模型的强假设是：

Quote

因为 softmax 是单调的，任何特征的增大都会导致模型输出的增大（如果对应的权重为正），或者导致模型输出的减小（如果对应的权重为负）

例子：对于图像识别，像素值反转，其实分类的物体应该是不变的，线性模型就失去了预测能力

2. 隐藏层与激活函数

考虑在网络中加入一个隐藏层，仅仅这样是不够的，因为这样本质还是线性函数

O = (X W^{(1)} + b^{(1)}) W^{(2)} + b^{(2)} = X W^{(1)} W^{(2)} + b^{(1)} W^{(2)} + b^{(2)} = X W + b .

加入激活函数 $σ$ 后会变成非线性函数:

\begin{array}{r} \begin{aligned} H & = σ (X W^{(1)} + b^{(1)}), \\ O & = H W^{(2)} + b^{(2)} . \end{aligned} \end{array}

一个单隐藏层的多层感知机，具有 5 个隐藏单元

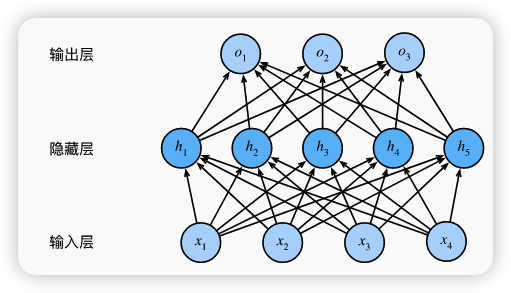
3. 通用近似原理

1989 年，George Cybenko 最早提出并证明了单一隐藏层、任意宽度、并使用 S 函数作为激励函数的前馈神经网络的通用近似定理：一个单隐层网络能学习任何函数，但并不意味着我们应该尝试使用单隐藏层网络来解决所有问题。事实上，通过使用更深（而不是更广）的网络，我们可以更容易地逼近许多函数。^[1]

思考：为什么不用单隐藏层来训练所有模型？

实际上做不到，而 CNN、RNN 目的就是人为的帮助神经网络提供一些数据本身时间、空间的信息，更有效的训练网络
尽管单层神经网络有能力拟合任何函数，但要达到这样的拟合可能需要非常多的神经元，并且可能不是最高效的方法。此外，当函数变得复杂时，单层网络可能很难训练，容易陷入局部最小值，而多层网络（深度网络）可以使用更少的参数更有效地逼近相同的函数，并且通常更容易训练。

4. 各种激活函数

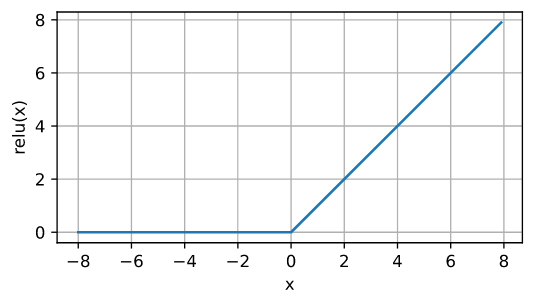
4.1 ReLU 函数

最受欢迎的激活函数是_修正线性单元_（Rectified linear unit，ReLU），因为它实现简单，同时在各种预测任务中表现良好。 ReLU 提供了一种非常简单的非线性变换。

提示

虽然在大于 0 时，ReLU 是线性的，但线性的概念是指输出随着输入线性变化，这种截断破坏了线性性

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))

ReLU (x) = max (x, 0) .

输入为 0 时导数为 0，实际情况输入可能永远都不会是0

4.2 sigmoid 函数

sigmoid (x) = \frac{1}{1 + \exp (- x)} .

y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

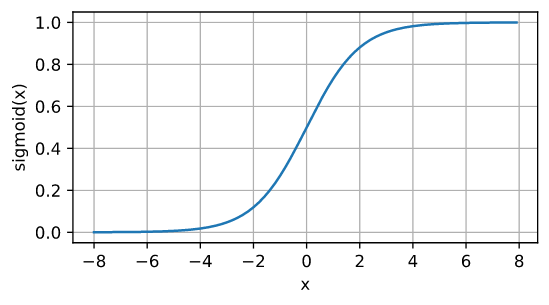
!center Sigmoid 导数图像，最大值 0.25，所以会出现梯度消失

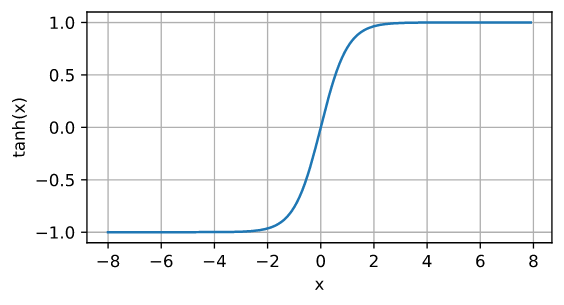
4.3 tanh 函数

\tanh (x) = \frac{1 - \exp (- 2 x)}{1 + \exp (- 2 x)} .

y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))

参考文献

https://www.jiqizhixin.com/articles/2021-09-07-6 ↩︎