4.2 多层感知机的从零开始实现

要点

这里的从零开始指的是自己完成参数，模型，激活函数定义
输出层神经元个数，和分类类别是一致的

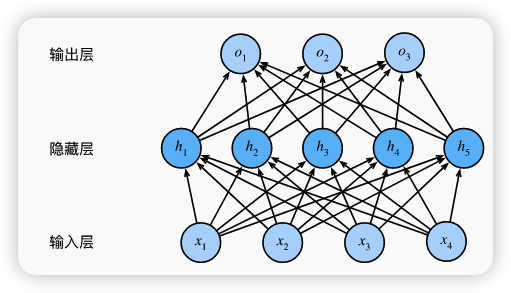
1. 初始化模型

具有一个隐藏的网络架构

4.1 多层感知机.png|center 一个单隐藏层的多层感知机，具有 5 个隐藏单元

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

参数维度：

$W_{1}$ ：(784, 256)
$b_{1}$ : (256,)
$W_{2}$ : (256,10)
$b_{2}$ : (10,)

注意：这里与内置的 `nn.linear` 参数是互为转置的

在许多机器学习和数学文献中, 线性变换通常是以列向量形式的输入 $x$ 和矩阵 $W$ 表达的，即 $y = W x + b$ 。在这种情况下， $W$ 的形状通常是 (输出维度, 输入维度)。然而, 在数据科学和机器学习的实践中, 特别是当涉及到批量处理时, 输入数据通常被组织成行向量形式的矩阵（每一行一个样本，因为大多数表都是纵表)。因此, 对于批量输入 $X$ , 线性变换需要被重新编写为 $Y = X W^{T} + b$ 以保持形状的一致性。

结论：

nn.Linear 的参数形状是 (out_features,in_features)，满足 $Y = X W^{T} + b$ 的情形

2. 激活函数

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

3. 定义模型

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

4. 损失函数

交叉熵损失：

loss = nn.CrossEntropyLoss(reduction='none')

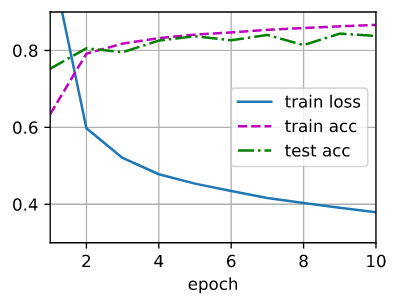
5. 训练

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

d2l.train_ch3 参考:

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad() # torch 的 SGD 学习器不会除以 batch_size
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0]) # 课程内置的 SGD 会除以 batch_size
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

1. 初始化模型

结论：

2. 激活函数

3. 定义模型

4. 损失函数

5. 训练

参考文献