4.8 数值稳定性和模型初始化
- 合理的权重初始值和激活函数的选取可以提升数值稳定性
- Xavier 初始化把神经元的值、参数和参数的梯度当做随机变量,研究传播过程中神经元值、神经元处梯度的变化,用来选取合理的初始值,保持神经元参数、神经元梯度大小的期望与方差不变
- 数值稳定指的是各个节点的神经元的值(和梯度)不会太大也不会太小
1. 神经网络的梯度

向量关于向量的导数是矩阵,矩阵关于矩阵的导数是张量
神经网络中神经元的值很大,正向传播会计算不下去,而神经元越大,该神经元的梯度有可能越大,例如:假设我们有一个单层神经网络, 它只有一个神经元和一个权重。我们将使用线性激活函数
现在, 我们希望最小化损失函数
按照链式法则, 我们有:
其中,
将这两个导数相乘, 我们得到:
从这个公式中, 我们可以看到, 如果输入
所以我们要尽量控制神经元的值不能太大,也不能太小(太小会出现梯度消失)


2. 梯度爆炸、梯度消失出现的问题


3. 训练更加稳定的几种方法
- 乘法变加法
- 例如 ResNet、LSTM
- 归一化
- 梯度归一化,梯度裁剪
- 合理的权重初始化(见下方)
3.1 Xavier 初始化
为了解决梯度爆炸问题,我们希望把每一层的梯度控制在一个合理范围内(固定期望的方差的范围),我们研究一下梯度在每层之间的流动:
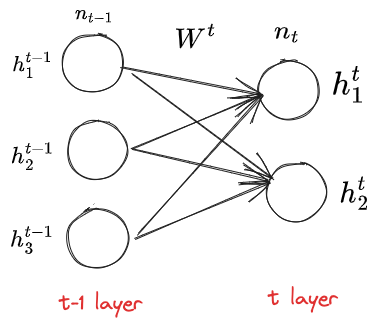
有以下三点假设,对于某固定第
是 i.i.d 的, 是 i.i.d 的 独立于
- 第一点:参数是我们可以控制的,所以我们做了一个简单的假设
- 第二点:输入的特征之间是独立的,这也是一个较强的假设(例如训练样本为图像,相邻之间的像素往往不是独立的,但像素比较多,近似可以认为两两独立)
- 第三点:当前层的参数与输入的特征无关,这也很好理解,因为当前层输入是上一层的参数决定的
- 这里对
只是要求独立,对值的分布没有要求
正向传播数值分布
正向传播的基本公式是:
现在计算 t 层激活函数值的期望与方差:
注意
反向传播数值分布
根据链式法则:
反向传播正向传播本质都是矩阵乘法,上面等式两边是 Jacobian matrix,矩阵大小:
把
与 正向传播是类似的,若要梯度在传播时保持均值,方差不变,则需要:
根据归纳法,我们只需要设定初始的参数值就可以,从而在传播过程中保持数值的稳定性
注意到(1)、(2)式子难以同时满足,为了做一个权衡:
所以每一层的参数按照以下分布进行初始化:
- 正态分布
- 均匀分布
分布
加上激活函数

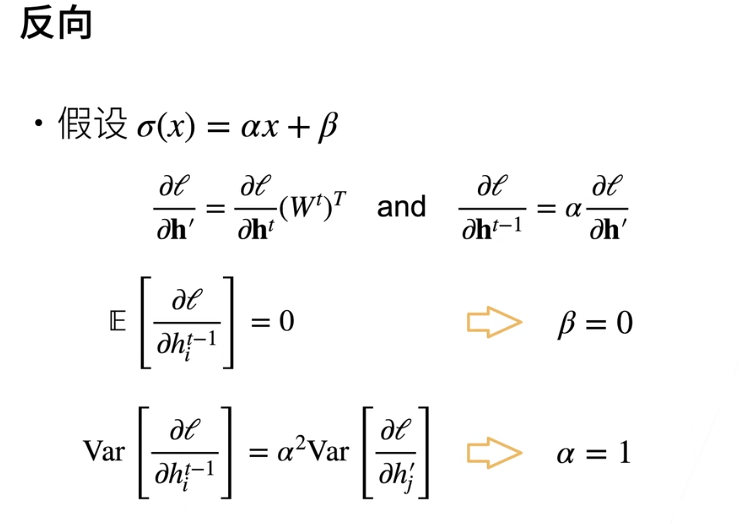
假设激活函数是线性的,要满足传播过程中正向和反向数值稳定,方差不会变化太大,则要求线性函数只能是
- 过原点
- 0 点导数为 1

4. 打破对称性
考虑一个只有两个神经元的隐藏层,这两个神经元如果初始化的时候参数一致,向前传播的参数值大小是一致的,向后传播对于参数的更新也是一致的,由于对称性这两个神经元本质没有什么不同(等价于一个神经元),所以在初始化的时候避免参数取值一致
随机梯度下降无法打破对称性,因为对于参数的更新还是对称的,dropout 可以打破对称性,原因是训练的时候随机关闭了一些神经元(参考 [[4.6 Dropout]])