6.4 多输入多输出通道
- 输出通道数是卷积层另一个超参数
卷积层忽略图像空间信息,等价于全连接层,通常用于调整网络层的输出通道数和控制模型复杂性。 - 每个输入通道都有对应的二维卷积和,所有通道计算结果求和得到一个单通道输出
- 每个输出通道具有独立的三维卷积核
- 通常来说如果图片大小减半了,通道个数就会翻倍
这里都是指只有高宽的二维卷积 Conv2d
一张图片里一般会有色彩信息,彩色图像具有标准的 RGB 通道来代表红、绿和蓝。当我们添加通道时,我们的输入和隐藏的表示都变成了三维张量。例如,每个 RGB 输入图像具有
1. 多输入通道
假设输入的通道为
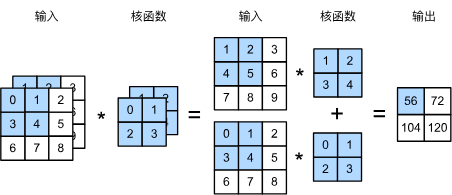
两个输入通道的互相关计算,卷积核输入通道为 2,需要与上一层样本输入通道一致
import torch
from d2l import torch as d2l
def corr2d_multi_in(X, K):
# 先遍历“X”和“K”的第0个维度(通道维度),再把它们加在一起
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
d2l.corr2d 的实现查看 6.2 图像卷积#^842cfd
上面代码实现多通道输入,单通道输出,zip 函数见 Python 中的 zip 函数,最后按元素求和,对上面图片的三维张量进行验证:
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
corr2d_multi_in(X, K)
tensor([[ 56., 72.],
[104., 120.]])
2. 多输出通道
由于多通道卷积核总是会压缩为单通道,我们对于卷积核还可以额外构造一维通道,叫做输出通道,保证输出的样本也是多通道的,使得训练更深
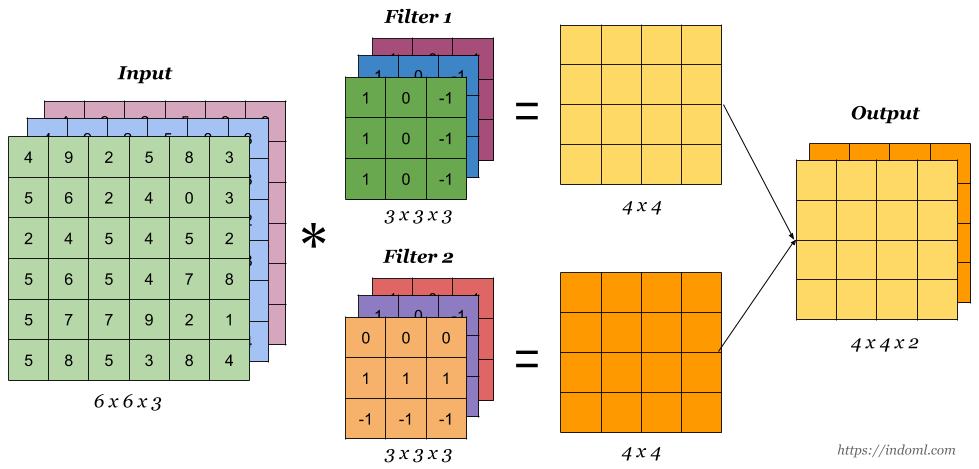

def corr2d_multi_in_out(X, K):
# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。
# 最后将所有结果都叠加在一起
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
torch.stack 会增加新的维度来堆叠张量, 假设有两个形状为 [A, B] 的张量,使用 torch.stack 并指定新维度为 0,那么输出的张量将会有形状 [2, A, B]
torch.cat 不改变原来张量的维度,而 torch.stack 通过堆叠来增加维度,例如:
import torch
a = torch.tensor([1, 2])
b = torch.tensor([3, 4])
# 沿第0维(维度索引从0开始)连接
result_cat = torch.cat((a, b), dim=0)
# 在新的维度上堆叠
result_stack = torch.stack((a, b), dim=0)
print(result_cat) # 输出:tensor([1, 2, 3, 4])
print(result_stack)
# 输出:
# tensor([[1, 2],
# [3, 4]])K = torch.stack((K, K + 1, K + 2), 0) #构造输出维度为三维
K.shape
X.shape
torch.Size([3, 2, 2, 2]) # 输出通道 3、输入通道 2、核大小 2x2
torch.Size([2, 3, 3]) # 输入通道 2、图片大小 3x3
3.
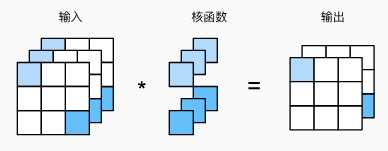
上图输入通道为 3,输出通道为 2,把空间位置打散,等价于输入形状为
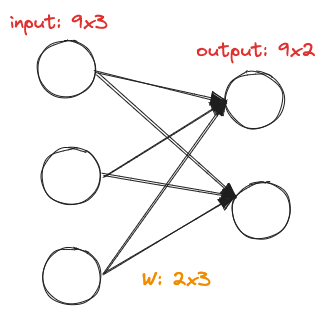
4. 二维卷积层总结
输入通道数 input channel 输出通道数 output channel 输入图片的高 输入图片的宽 核的高 核的宽 输出图片的高,由输入、核、步幅决定(参考 [[6.3 填充和步幅]]) 输出图片的宽,由输入、核、步幅决定(参考 [[6.3 填充和步幅]])
- 以上这些只有输出的通道数是超参数,因为输入通道数是上一层决定的,其他的参数都与核大小有关
- 输入
- 核
- (注意:PyTorch 里位置是相反的:
nn.Conv2d(in_channels, out_channels, kernel_size))
- (注意:PyTorch 里位置是相反的:
- 偏差
- 输出
- 计算复杂度 (浮点计算数 FLOP)
)
- 10 层,
样本, 10 PFlops
下面的代码验证
# 验证 1x1 的卷积是不是全连接层
def corr2d_multi_in_out_1x1(X, K):
c_i, h, w = X.shape
c_o = K.shape[0]
X = X.reshape((c_i, h * w))
K = K.reshape((c_o, c_i))
# 全连接层中的矩阵乘法
Y = torch.matmul(K, X)
return Y.reshape((c_o, h, w))
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6