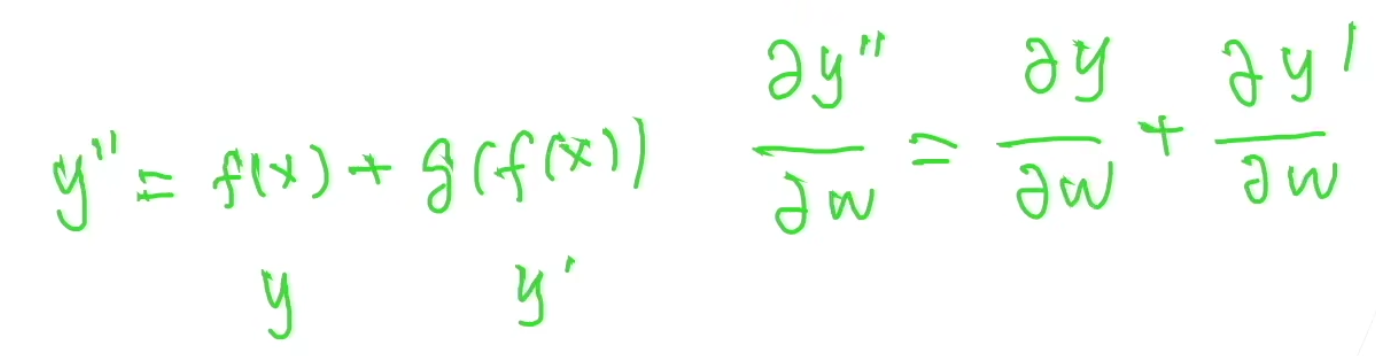7.6 残差网络(ResNet)
- 每一个带 1x1 的ResNet块,使得图像高宽减半,通道翻倍
- ResNet18 模型大约是 18M,和 AlexNet 相比小很多(全连接层),但计算量比 AlexNet 大(不能简单认为模型参数越大,计算越复杂)
1. 深度神经网络与函数类
当网络越来越深的时候,我们要思考的一个问题是,越深的网络真的越有效吗?
答案是否定的,训练神经网络可以看做在一个泛函空间中寻找最合适的函数
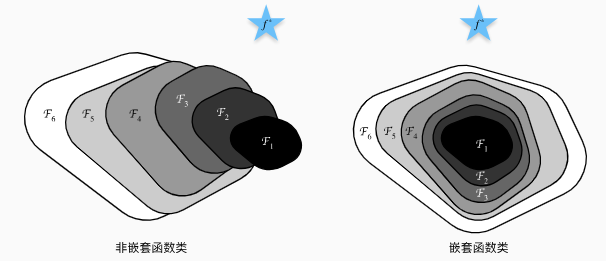
虽然根据通用近似原理 ([[4.1 多层感知机 MLP#^faa02c]]),单层网络具有拟合任何函数的能力,上图指的是在相同训练成本下模型能达到的边界
考虑一个简单的两层全连接神经网络:
假设激活函数
所以我们设计网络结构时,下一层是上一层的嵌套函数类,这样增加网络层数使得训练是有效的
2. 残差块
一种思想是在恒等映射的基础上加上原来的神经网络,使得函数具备这种嵌套能力
这样第二层神经元就具有拟合原输入
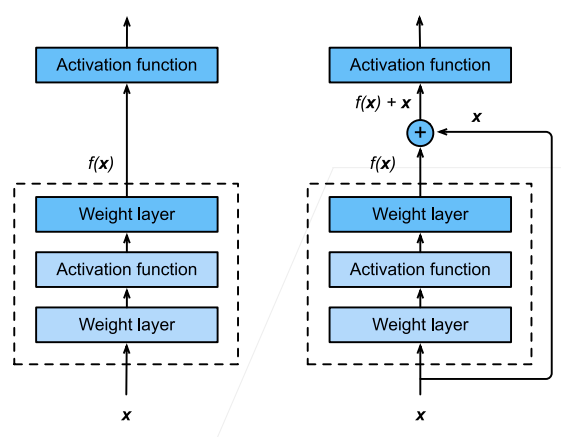
ResNet 块利用 7.2 使用块的网络(VGG)的设计,加入了 7.5. 批量规范化,有时直接并联需要利用
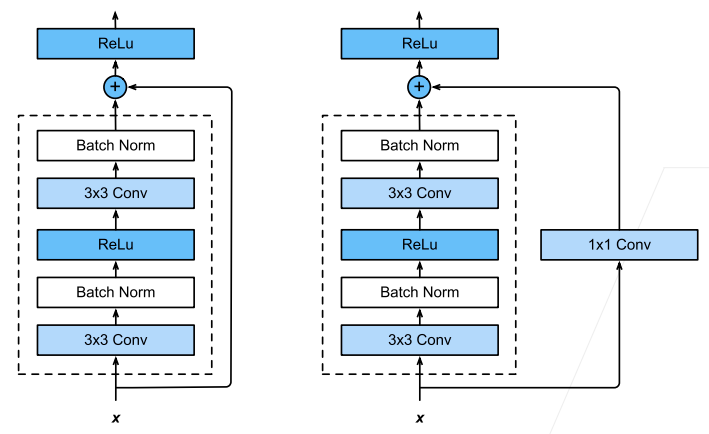
也可以调整并联位置来设计不同的残差块
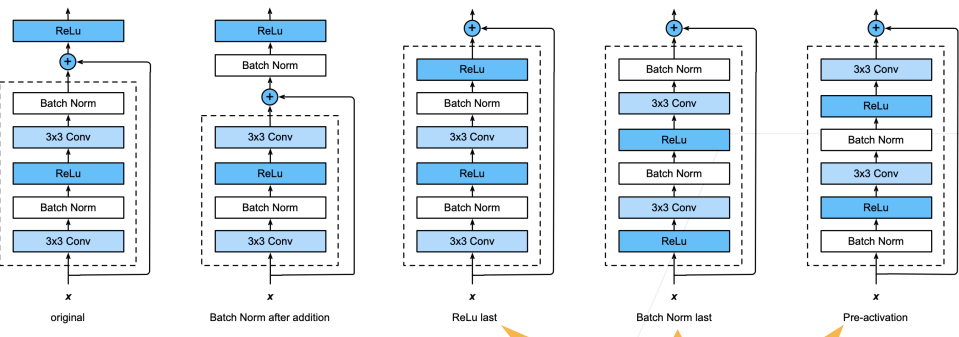
具体实现:
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Residual(nn.Module): #@save
def __init__(self, input_channels, num_channels,
use_1x1conv=False, strides=1): # 如果input_channels == num_channels,use_1x1conv=False
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels,
kernel_size=3, padding=1, stride=strides) # 第一个 3x3 卷积调整通道
self.conv2 = nn.Conv2d(num_channels, num_channels,
kernel_size=3, padding=1) # 第二个 3x3 卷积不改变通道数
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return F.relu(Y)
blk = Residual(3,6,use_1x1conv=True,strides=2) # 批大小 4,输入通道 3,输出通道 30,图像大小减半
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape # torch.Size([4, 6, 3, 3])
3. ResNet 模型
3.1 ResNet 块
残差块的组合称为 ResNet 块
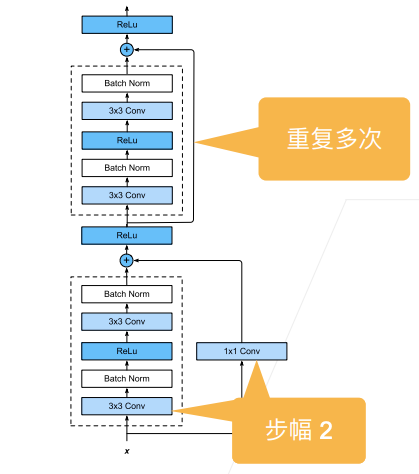
- 第一个残差块图像大小减半,通道数翻倍
- 第二个残差块不改变图像大小、通道数
def resnet_block(input_channels, num_channels, num_residuals,
first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block: # 第一个残差块是不改变通道数的,下图 b2
blk.append(Residual(input_channels, num_channels,
use_1x1conv=True, strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
3.2 ResNet-18 架构
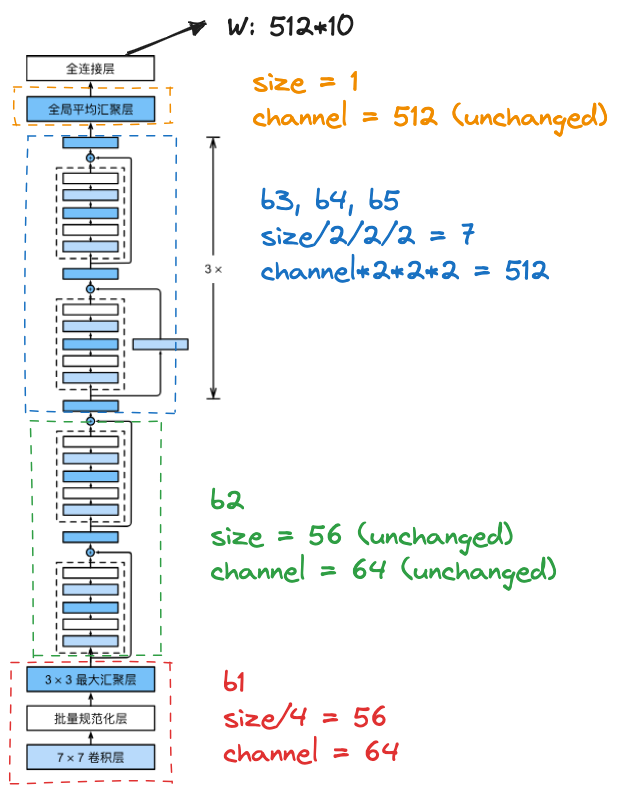
b2-5 每个都有 4 个卷积,加上 b1 的两个,一共是 18 个,所以叫做 ResNet-18
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))
net = nn.Sequential(b1, b2, b3, b4, b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(), nn.Linear(512, 10)) # 10 表示数据集的 10 个类别
这里的 * 是解包 Python中的与**用法#^67ec1f
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape:\t', X.shape)
Sequential output shape: torch.Size([1, 64, 56, 56])
Sequential output shape: torch.Size([1, 64, 56, 56])
Sequential output shape: torch.Size([1, 128, 28, 28])
Sequential output shape: torch.Size([1, 256, 14, 14])
Sequential output shape: torch.Size([1, 512, 7, 7])
AdaptiveAvgPool2d output shape: torch.Size([1, 512, 1, 1])
Flatten output shape: torch.Size([1, 512])
Linear output shape: torch.Size([1, 10])
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
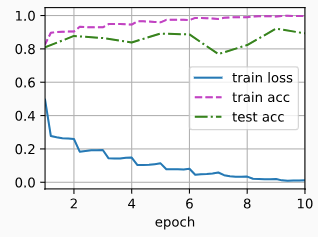
loss 0.012, train acc 0.997, test acc 0.893
5032.7 examples/sec on cuda:0
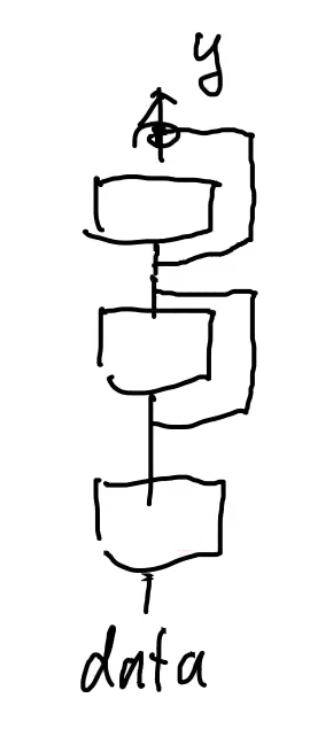
4. ResNet 为什么可以训练出 1000 层网络
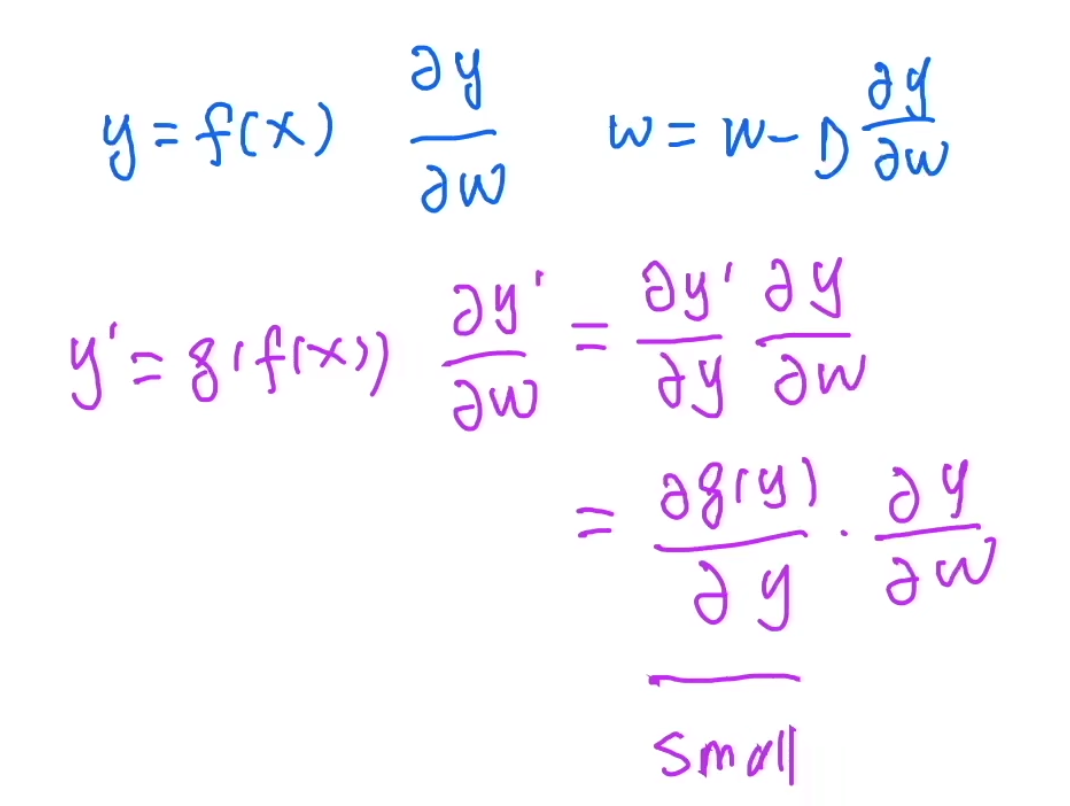
如上图,假如我有两层神经网络,计算第一层的梯度是第二层累乘过来的,一般来说,随着训练进行,损失函数越小,第二层的梯度会很小(一个全连接层+一个凸的 loss 是一个凸函数),由于乘法计算,传播到第一层的梯度就会很小,导致靠近输入端的参数难以训练