8.3 语言模型和数据集

要点

基于马尔科夫假设，介绍了 N-gram 模型
介绍了基于文本生成特征的的 SeqDataLoader 类：
- 随机生成：批和批之间不是连续的，完全独立的
- 顺序生成：批和批之间是连续的（一个批内的样本不一定连续）

1. N-gram 模型介绍

给定文本序列 $x_{1}, \dots, x_{T}$ , 语言模型的目标是估计联合概率 $p (x_{1}, \dots, x_{T})$
它的应用包括
- 做预训练模型 (eg BERT, GPT-3)
- 生成本文, 给定前面几个词, 不断的使用 $x_{t} \sim p (x_{t} ∣ x_{1}, \dots, x_{t - 1})$ 来生成后续文本
- 判断多个序列中哪个更常见, e.g. “to recognize speech” vs "to wreck a nice beach

由条件概率公式：

p (x_{1}, x_{2}, \dots, x_{m}) = p (x_{1}) * p (x_{2} ∣ x_{1}) * p (x_{3} ∣ x_{1}, x_{2}) \dots p (x_{m} ∣ x_{1}, \dots, x_{m - 1})

注意

这里 $x_{1}, x_{2}, \dots, x_{m}$ 是有顺序的，例如 $p (你, 好) \neq p (好, 你)$ 也就是说：

p (x_{1}, x_{2}) \neq p (x 2, x 1)

这个概率随着长度增加越来越不好算，假设后面生成的词只和当前词的前几个词有关（类似于卷积的局部性 6.2 图像卷积#^df8b77）, 和序列模型一样（8.1 序列模型），取决于具体和前几个词有关：

一元语法（词和词之间是独立的）:

\begin{aligned} p (x_{1}, x_{2}, x_{3}, x_{4}) & = p (x_{1}) p (x_{2}) p (x_{3}) p (x_{4}) \\ = \frac{n (x_{1})}{n} \frac{n (x_{2})}{n} \frac{n (x_{3})}{n} \frac{n (x_{4})}{n} \end{aligned}

二元语法（当前词与前一个词有关）：

\begin{aligned} p (x_{1}, x_{2}, x_{3}, x_{4}) & = p (x_{1}) p (x_{2} ∣ x_{1}) p (x_{3} ∣ x_{2}) p (x_{4} ∣ x_{3}) \\ = \frac{n (x_{1})}{n} \frac{n (x_{1}, x_{2})}{n (x_{1})} \frac{n (x_{2}, x_{3})}{n (x_{2})} \frac{n (x_{3}, x_{4})}{n (x_{3})} \end{aligned}

三元语法 (当前词与前两个词有关):

p (x_{1}, x_{2}, x_{3}, x_{4}) = p (x_{1}) p (x_{2} ∣ x_{1}) p (x_{3} ∣ x_{1}, x_{2}) p (x_{4} ∣ x_{2}, x_{3})

所以 N-gram 语言模型可以找到任意序列的概率，从而生成文本

总结

不管 n 是几，都要计算 4 次来计算 $p (x_{1}, x_{2}, x_{3}, x_{4})$ 的值
二元语法要知道任意两个词出现的概率，随着 $n$ 的增加， $n (x_{1}, x_{2}, x_{3} \dots)$ 的个数呈指数上升

2. 时间与空间复杂度

时间复杂度：

实际上，对于 $n$ 阶的马尔科夫模型，就是不停地计算上面的条件概率，假设我想知道 $p (x_{1}, \dots, x_{T})$ ，我需要计算 $T$ 次（上面的例子为 4），每次计算条件概率只需要 $O (1)$ 的复杂度，所以时间复杂度为 $O (T)$ ， $T$ 为生成文本的大小

这里把 $n (x_{1}, x_{2}, x_{3} \dots)$ 都存下来，可以利用哈希算法降低查找的复杂度

空间复杂度

因为随着模型阶数增加，例如我语料中有 10 个词，二元词组就有 100 个， $n (x_{1}, x_{2}, x_{3} \dots)$ 的个数呈指数上升，所以空间复杂度为 $O (V^{n})$ ，其中 $V$ 是词汇量， $n$ 是模型阶数

3. 文本词频分布

时光机器数据集构建词表，并打印前10个最常用的（频率最高的）单词与频率分布

import random
import torch
from d2l import torch as d2l

tokens = d2l.tokenize(d2l.read_time_machine())
# 因为每个文本行不一定是一个句子或一个段落，因此我们把所有文本行拼接到一起
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]

[('the', 2261),
 ('i', 1267),
 ('and', 1245),
 ('of', 1155),
 ('a', 816),
 ('to', 695),
 ('was', 552),
 ('in', 541),
 ('that', 443),
 ('my', 440)]

大部分都是没有实际意义的词，叫做停用词（stop words），继续在双对数坐标下画出频率分布：

freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',
         xscale='log', yscale='log')

词频满足幂律分布
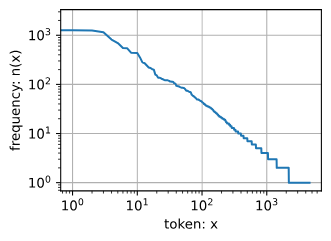
对多元词组也计算一下分布：

bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]

[(('of', 'the'), 309),
 (('in', 'the'), 169),
 (('i', 'had'), 130),
 (('i', 'was'), 112),
 (('and', 'the'), 109),
 (('the', 'time'), 102),
 (('it', 'was'), 99),
 (('to', 'the'), 85),
 (('as', 'i'), 78),
 (('of', 'a'), 73)]

trigram_tokens = [triple for triple in zip(
    corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
trigram_vocab.token_freqs[:10]

[(('the', 'time', 'traveller'), 59),
 (('the', 'time', 'machine'), 30),
 (('the', 'medical', 'man'), 24),
 (('it', 'seemed', 'to'), 16),
 (('it', 'was', 'a'), 15),
 (('here', 'and', 'there'), 15),
 (('seemed', 'to', 'me'), 14),
 (('i', 'did', 'not'), 14),
 (('i', 'saw', 'the'), 13),
 (('i', 'began', 'to'), 13)]

三元词组停用词更少一点，我们直观地对比三种模型中的词元频率：一元语法、二元语法和三元语法。

bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',
         ylabel='frequency: n(x)', xscale='log', yscale='log',
         legend=['unigram', 'bigram', 'trigram'])

多元词组同样满足幂律分布

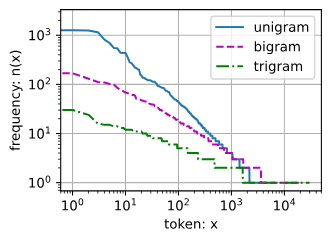
由于幂律分布，极少数词就包含了文本绝大多数词汇，所以 n 元语法空间复杂度并不会出现指数上升，这也是有些文章做到 7 元语法的原因

4. 读取文本序列数据

类似于序列模型，我们想从文本中构建特征，由于马尔科夫假设，我们可以固定窗口大小，如果滑动窗口步长为 1 去抽取特征。这样成本太高，如果我们头开始不相交的抽取文本，有些序列又覆盖不了:
如果按 A 的方法抽取特征，则覆盖不了 B 红色部分那个特征，正确方法应该是随机舍去一些开头部分的数据达到随机抽取的目的

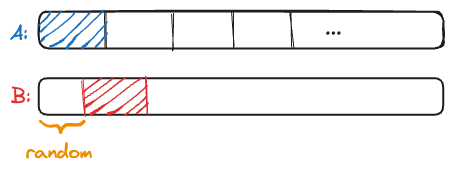
所以，为了保证尽量覆盖所有序列，尽量避免重复使用序列，我们随机把前面部分删去一点，开始不相交的抽取特征，抽取有两种方法，随机和顺序：
随机（左）和顺序（右）抽取特征，对于 0-34 的数组，一共可以抽取 6 个，两次随机都是截取 3 开始，batch_size=2，num_steps=5

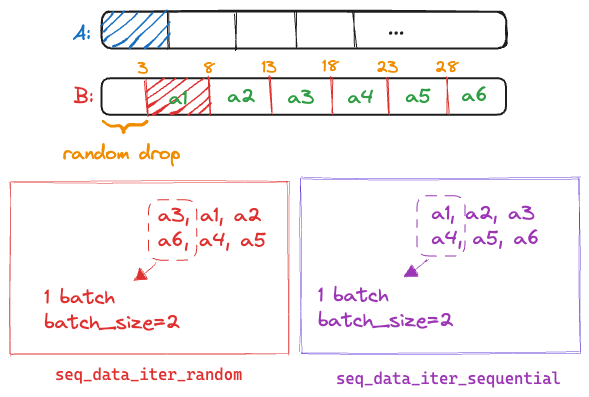
随机采样每个批次的样本之前是独立的
顺序采样每个批之间是连续的
一共可抽取 $⌊ (35 - 1) / 5 ⌋ = 6$ ，下面代码第六行，为什么这里要 $- 1$ ，是因为留一位抽取 y，例如[0,1,2,3] 抽取 num_steps=2 的序列只能抽 1 个，因为抽 [2,3] 就没有对应的 y 了

4.1 随机采样

def seq_data_iter_random(corpus, batch_size, num_steps):  #@save
    """使用随机抽样生成一个小批量子序列"""
    # 从随机偏移量开始对序列进行分区，随机范围包括num_steps-1
    corpus = corpus[random.randint(0, num_steps - 1):]
    # 减去1，是因为我们需要考虑标签
    num_subseqs = (len(corpus) - 1) // num_steps
    # 长度为num_steps的子序列的起始索引
    initial_indices = list(range(0, num_subseqs * num_steps, num_steps))
    # 在随机抽样的迭代过程中，
    # 来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻
    random.shuffle(initial_indices)

    def data(pos):
        # 返回从pos位置开始的长度为num_steps的序列
        return corpus[pos: pos + num_steps]

    num_batches = num_subseqs // batch_size
    for i in range(0, batch_size * num_batches, batch_size):
        # 在这里，initial_indices包含子序列的随机起始索引
        initial_indices_per_batch = initial_indices[i: i + batch_size]
        X = [data(j) for j in initial_indices_per_batch]
        Y = [data(j + 1) for j in initial_indices_per_batch]
        yield torch.tensor(X), torch.tensor(Y)

num_steps 序列 X 的特征个数
batch_size：一个批中包含的样本数

my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):
    print('X: ', X, '\nY:', Y)

my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):
    print('X: ', X, '\nY:', Y)

X:  tensor([[13, 14, 15, 16, 17],
        [28, 29, 30, 31, 32]])
Y: tensor([[14, 15, 16, 17, 18],
        [29, 30, 31, 32, 33]])
X:  tensor([[ 3,  4,  5,  6,  7],
        [18, 19, 20, 21, 22]])
Y: tensor([[ 4,  5,  6,  7,  8],
        [19, 20, 21, 22, 23]])
X:  tensor([[ 8,  9, 10, 11, 12],
        [23, 24, 25, 26, 27]])
Y: tensor([[ 9, 10, 11, 12, 13],
        [24, 25, 26, 27, 28]])

注意

这里的 Y 不是向量，而是 X 往后移一位的矩阵

4.2 顺序采样

def seq_data_iter_sequential(corpus, batch_size, num_steps):  #@save
    """使用顺序分区生成一个小批量子序列"""
    # 从随机偏移量开始划分序列
    offset = random.randint(0, num_steps)
    num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
    Xs = torch.tensor(corpus[offset: offset + num_tokens])
    Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])
    Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
    num_batches = Xs.shape[1] // num_steps
    for i in range(0, num_steps * num_batches, num_steps):
        X = Xs[:, i: i + num_steps]
        Y = Ys[:, i: i + num_steps]
        yield X, Y

for X, Y in seq_data_iter_sequential(my_seq, batch_size=2, num_steps=5):
    print('X: ', X, '\nY:', Y)

X:  tensor([[ 3,  4,  5,  6,  7],
        [18, 19, 20, 21, 22]]) 
Y: tensor([[ 4,  5,  6,  7,  8],
        [19, 20, 21, 22, 23]])
X:  tensor([[ 8,  9, 10, 11, 12],
        [23, 24, 25, 26, 27]]) 
Y: tensor([[ 9, 10, 11, 12, 13],
        [24, 25, 26, 27, 28]])
X:  tensor([[13, 14, 15, 16, 17],
        [28, 29, 30, 31, 32]]) 
Y: tensor([[14, 15, 16, 17, 18],
        [29, 30, 31, 32, 33]])

4.3 整合成 `SeqDataLoader` 类

类似于 DataLoader 类 Pytorch 用法#^a5f724，封装成一个可迭代对象（Python 中的可迭代对象、迭代器#^89a039）

class SeqDataLoader:  #@save
    """加载序列数据的迭代器"""
    def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):
        if use_random_iter:
            self.data_iter_fn = d2l.seq_data_iter_random
        else:
            self.data_iter_fn = d2l.seq_data_iter_sequential
        self.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)
        self.batch_size, self.num_steps = batch_size, num_steps

    def __iter__(self):
        return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)

这里的 max_tokens 是防止序列过大做一个限制，整合在一起可以读取序列数据：

def load_data_time_machine(batch_size, num_steps,  #@save
                           use_random_iter=False, max_tokens=10000):
    """返回时光机器数据集的迭代器和词表"""
    data_iter = SeqDataLoader(
        batch_size, num_steps, use_random_iter, max_tokens)
    return data_iter, data_iter.vocab

1. N-gram 模型介绍

2. 时间与空间复杂度

时间复杂度 ：

空间复杂度

3. 文本词频分布

4. 读取文本序列数据

4.1 随机采样

4.2 顺序采样

4.3 整合成 SeqDataLoader 类

参考文献

时间复杂度：

4.3 整合成 `SeqDataLoader` 类