9.1 门控循环单元(GRU)
- GRU 可以通过更新门维护梯度流,相对普通 rnn 可以学习更长的序列,但一般也不超过100
在 rnn 中,每次都是都把过去的总结更新为隐状态,过去的每个观察不是同等都很重要的:

门控循环单元(gated recurrent unit,GRU) (Cho et al., 2014) 是 LSTM 一个稍微简化的变体,通常能够提供 LSTM 同等的效果,并且计算 (Chung et al., 2014)的速度明显更快。
1. 门控隐状态
1.1重置门和更新门
我们首先介绍重置门(reset gate)和更新门(update gate)。我们把它们设计成 (0,1)区间中的向量,这样我们就可以进行凸组合。
- 重置门允许我们控制“可能还想记住”的过去状态的数量;
- 更新门将允许我们控制新状态中有多少个是旧状态的副本。
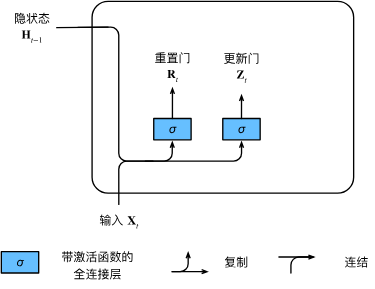
我们来看一下门控循环单元的数学表达。对于给定的时间步
实际上等价于 RNN 中(8.4 循环神经网络)隐状态的构造。其中
1.2 候选隐藏状态
确定当前
其中
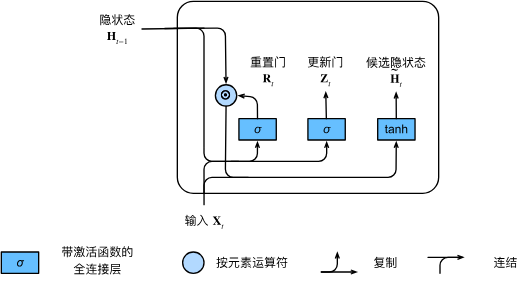
:当前时间点的信息很重要,过去的状态全部被遗忘(重置) :普通的循环神经网络
1.3 确定隐状态
上述的计算结果只是候选隐状态, 我们仍然需要结合更新门
这些设计可以帮助我们处理循环神经网络中的梯度消失问题(类似于 ResNet 7.6 残差网络(ResNet)), 并更好地捕获时间步距离很长的序列的依赖关系。例如, 如果整个子序列的所有时间步的更新门都接近于 1 , 则无论序列的长度如何, 在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。
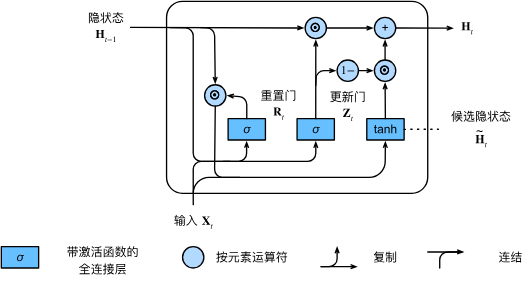
:接近候选隐藏状态(由 控制当前时间点重要程度) :过去状态很重要,当前时间点完全遗忘
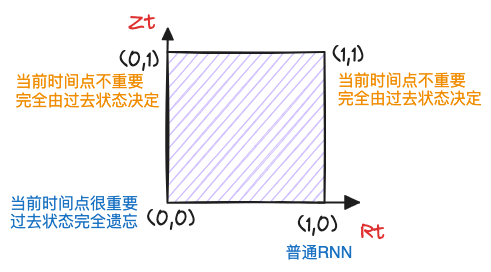
如上图所示,实际上序列大部分都是重复以前发生的信息,所以当前信息对隐状态更新效果比较小,而发生大事件才会造成过去状态的重置
2. 从 0 开始实现 GRU
import torch
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
2.1 初始化模型参数
def get_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device)*0.01
def three():
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xz, W_hz, b_z = three() # 更新门参数
W_xr, W_hr, b_r = three() # 重置门参数
W_xh, W_hh, b_h = three() # 候选隐状态参数
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
本质上和普通 RNN 的参数初始化没区别,更新门、重置门本质就是和状态维度一样的软控制参数
2.2 定义模型
def init_gru_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), )
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = H @ W_hq + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H,)
*表示元素级别的乘法@矩阵乘法,与torch.mul一致
2.3 训练与预测
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,
init_gru_state, gru)
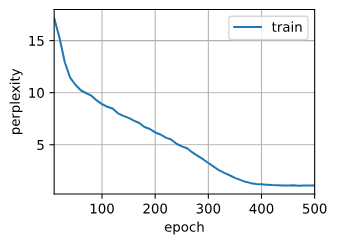
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
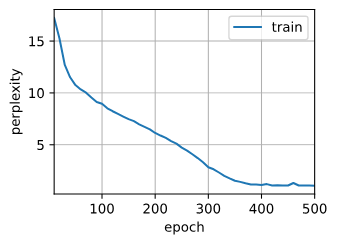
perplexity 1.1, 10510.3 tokens/sec on gpu(0)
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby
3. GRU 简洁实现
和 rnn 类似(8.6 循环神经网络的简洁实现)
gru_layer = rnn.GRU(num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
perplexity 1.1, 183591.3 tokens/sec on gpu(0)
time traveller for so it will be convenient to speak of himwas e
travelleryou can show black is white by argument said filby